실습-11 반사경 안테나(Reflector Antenna)
반사경 안테나는 도체 평면에서의 전파의 입사각과 반사각이 동일하다는 반사의 법칙을 이용하여 넓은 면에 입사하는 전파를 한 점(초점)으로 모아서 수신하는 장치이다. 역으로 초점에서 방사된 전파는 반사경에 의해 반사된 후 반사경의 넓은 면적에 걸쳐 동시에 같은 방향으로 전파된다.
반사경 안테나는 구조의 단순성, 광대역 특성, 높은 효율, 크기를 증가시킴으로써 이득을 비례하여 증가시킬 수 있다는 장점으로 마이크로파 점대점 통신, 위성통신, 군용 레이더, 우주선 통신, 전파 천문학 등의 용도로 널리 사용되고 있다.
I. 실습
1. 원형 도파관 피드 설계
원형 도파관: 내경 직경 20mm, 외경 22mm (벽두께 1mm로 함), 길이 60mm
좌표계: 원점 = 개구면 중심, z 축 = 도파관 축과 평행하며 입력 포트에서 멀어지는 방향, y축 = 수직방향
여기: wave port, TE11 모드, 전기장 y축 방향
1) 형상
2) 포트 면에서의 전기장 분포, arrow plot, 14GHz
차단 주파수 = (
)GHz
3) 개구 면에서의 전기장 분포, arrow plot, 14GHz
4) 반사계수:
-40dB to 0dB, 10-20GHz
5) 1D 이득 패턴: Ludwig 3, Cartesian, 14GHz, -30dB to 15dB, -180º to 180º, 모두 동일한 그래프에
Co-pol. gain,
phi = 0º
Co-pol. gain,
phi = 90º
Cross-pol.
gain, phi = 45º
최대 이득 = (
)dB
-3dB 빔폭 (전계면/자계면 평균) = (
)º
-10dB 빔폭 (전계면/자계면 평균) = (
)º
6) 1D 위상 패턴: Ludwig 3, Cartesian, 14GHz, 0º to 360º, -180º to
180º, 모두 동일한 그래프에, 위상 패턴 계산 시 원거리 계산 자표 원점을 개구면 중심에 둘 것.
Co-pol.
phase, phi = 0º
Co-pol. phase, phi = 90º
7) 2D co-pol. 이득 패턴: Ludwig 2, 14GHz, magnitude range = automatic
8) 2D cross-pol. 이득 패턴: Ludwig 2, 14GHz, magnitude range = automatic
최대 이득 = (
)dB
2. 포물면 반사경 설계
반사경: 포물면, 직경 D = 314mm, 초점거리 F = 110mm, 금속 두께 = 1mm
피드: 위에서 설계한 원형 도파관. 위상 중심 = 개구면 중심
피드의 원거리 패턴을 계산하여 far-field source로 반사경을 조사
시뮬레이션: 1/4 등분하여 해석. electrical wall(전기장이 수직인 면), magnetic wall(자기장이 수직인 면) 개념 이해
yz-평면: 자기장이 수직, 전기장은 평행 → magnetic wall
zx-평면: 전기장이 수직, 자기장은 평행 → electric wall
1) 형상
F/D = ( )
피드 조사각 = (
)º
2) 1D 이득 패턴, 광각: Ludwig 3, Cartesian,
14GHz, -30dB to 40dB, -180º to 180º, 모두 동일한 그래프에
Co-pol. gain,
phi = 0º
Co-pol. gain,
phi = 90º
Cross-pol.
gain, phi = 45º
3) 1D 이득 패턴, 협각: Ludwig 3, Cartesian,
14GHz, -30dB to 40dB, -30º to 30º, 모두 동일한 그래프에
Co-pol. gain,
phi = 0º
Co-pol. gain,
phi = 90º
Cross-pol.
gain, phi = 45º
최대 이득 = ( )dB
-3dB 빔폭 (전계면/자계면 평균) = (
)º
부엽준위 = (
)dB
개구효율 = (
)%
빔폭계수 = (
)º
3) 2D co-pol. 이득 패턴: Ludwig 2, 14GHz, magnitude range = -30dB to 40dB (adjusted)
4) 2D cross-pol. 이득 패턴: Ludwig 2, 14GHz, magnitude range = automatic
최대 이득 = ( )dB
II. 이론
1. 반사 법칙
1) 반사 법칙(law of reflection)
- 도체 평면에서 전자파 반사
- 입사파 진행방향 벡터, 평면의 접선, 반사파 진행방향 벡터: 동일 평면 = 입사평면(plane
of incidence)
- 반사각은 입사각과 동일:
![]()
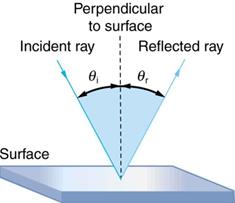
그림: 평면에서 전자파의 반사법칙
- 파장에 피해 표면 거칠기가 무시하지 못할 정도로 크면 반사파가 여러 방향으로 흩어진다. → rough surface scattering
- 반면에 표면 거칠기가 파장에 비해 매우 작을 경우는 평면에서의 반사 법칙이 성립한다.
- 이러한 경우를 specular
reflection이라 한다.
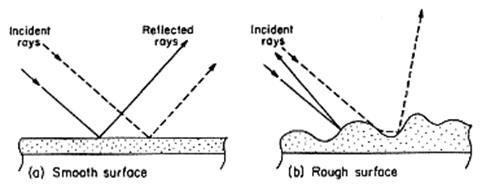
그림: (a) 매끄러운 면에서의 반사, (b) 거친 면에서의 반사 [OSA]
2) 부드러운 곡면에서의 반사
- 곡률 반경이 파장에 비해 매우 큰 부드러운 곡면에 전파가 입사할 경우 입사점에서 곡면을 지역적으로 평면과 같다고 가정하여 반사파의 방향을 구한다. 이 때 평면은 입사점에서 곡면에 접하는 평면(법선에 수직인 평면)이다.

그림: 곡면에서의 반사 법칙 [study.com]
2. 포물면 반사경(parabolic reflector)
1) 동작원리
- 개구에 수직(포물면 반사경 중심축에 평행)인 방향으로 입사하는 wave는 포물면에 반사된 후 한 점(초점)에 모인다.
- 위와 같이 동작하는 곡면을 수학적으로 유도하면 이차 곡선인 포물선을 회전하여 얻은 포물면(paraboloid)가 된다.
- 초점면(focal plane)에서 출발한 ray가 포물면에 반사된 후 초점에 도달하는 거리는 모두 동일하다.
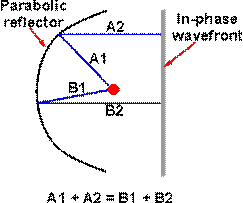
그림: 포물면 반사경의 동작원리
2) 이론

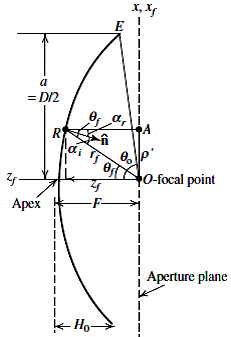
그림: 포물면 반사경 설계변수 [Stutzman]
ㅇ 좌표계
- 반사면 좌표계: 원점 = 초점, 반사경 중심축 = z 축 방향(+z 축 방향이 포물면에서 멀어지는 방향), zx 평면 = 수직 절단면
- 피드 좌표계: 구좌표계를 사용하는 것이 편리
![]() : 구좌표계
: 구좌표계
![]() : 원통좌표계
: 원통좌표계
![]()
ㅇ 설계변수
- 반사경 직경 D: 개구면 직경. 안테나 이득을 결정
- 초점거리 F: 반사경 안테나의 길이를 결정. F가 클수록 곡면에 평평해진다.
- F/D 비: 초점거리대 직경 비. 피드가 포물면을 조사하는 각도 범위 결정
ㅇ 용어
- Apex (= vertex): 포물면 중심점
- E : edge. 포물면 테두리
- H0 : 포물면 두께
ㅇ F/D에 따른 포물면 곡률: F/D가 클수록 반사면이 평평해진다.
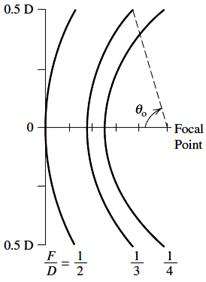
그림: F/D 비에 따른 포물면 평평도 [Stutzman]
ㅇ F/D에 따른 피드 조사각
![]()
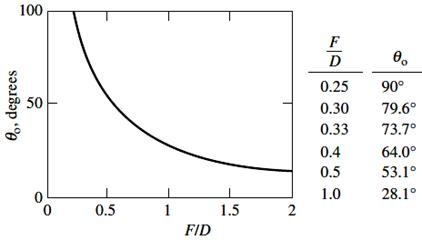
그림: F/D 비에 따른 피드 조사각 [Stutzman]
ㅇ 반사경 두께
- F/D가 클수록 두께가 작다.
![]()
![]()
2) 수학식
ㅇ 포물면
![]() : 직각 좌표계
: 직각 좌표계
![]() : 구 좌표계
: 구 좌표계
![]() : 원통-구 좌표계
: 원통-구 좌표계
ㅇ 개구면 전기장
![]()
![]()
![]()
![]()
ㅇ 피드 방사패턴
![]()
U, V: difficult to find for all angles
We use principal plane
(E- and H-plane) patterns and use interpolation for phi.
Feed is linearly
polarized.
![]() : principal plane pattern
: principal plane pattern
![]()
![]()
Balanced feed:
symmetrical secondary pattern and very low cross-polarization
![]()
![]()
![]()
General feed model
![]()
![]() : 피드 이득
: 피드 이득
ㅇ 방사패턴
1) Aperture integration
method
![]()

2) PO(physical optics)
method
![]() (on the front
surface of the reflector)
(on the front
surface of the reflector)
![]()
ㅇ 이득 공식
- 일반적인 안테나 이득 공식
![]()
e
: 개구 효율
Ap
: 방사면의 면적
- 원형 반사경 이득 공식
![]()
![]()
D
: 반사경 직경
반사경 안테나의 개구 효율: 보통 0.5-0.7. 정확하지 않으면 0.5 사용
- 효율에 따른 이득 감소
e e(dB)
1 0
0.9 -0.46
≈ -0.5
0.8 -0.97
≈ -1.0
0.7 -1.55
≈ -1.5
0.6 -2.22
≈ -2
0.5 -3.01
≈ -3
0.4 -3.98
≈ -4
0.3 -5.23 ≈ -5
ㅇ 빔폭 공식
![]()
K ≈
70º: 빔폭계수
III. 연습 문제
1. 10GHz 이득이 45dB인 포물면 반사경을 설계하라. 단, F/D = 0.4로 하라.
2. 위 안테나의 피드 조사각 θ0를 구하라.
3. 위 안테나의 빔폭(3dB 빔폭, 반치각)을 구하라.