Microwave Engineering Final Exam Solutions

학번 ( ) 성명 ( ) 이동전화번호 (010-8028-3194)

PIN = abcd = 3194, a = 3, b = 1, c = 9, d = 4

Total points = 120

1. C₁ = 10a (nF), L₁ = 100b (pH), R₁ = c/1000 (Ω), R₂ = 10d (GΩ). Neglect R₂ and R₁. Find the self-resonant frequency f_r (Hz). (10 points)

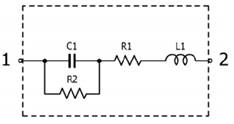
(Answer) 10 points

C₁ = 10a = 30 nF, L₁ = 100b = 100 pH

f_r = 1/[2π(L₁C₁)^1/2] = 1/[2π(100×10⁻¹²×30×10⁻⁹)^1/2] = 1/[2π(3×10⁻¹⁸)^1/2] = 10⁹/[2×3^1/2π] = 91.9 MHz

2. Parallel-plate capacitor

Plate area: S = a cm²

Plate separation: d = b/10 cm

f = 10 MHz

Real part of the complex permittivity filling the capacitor: ε' = cε₀

Imaginary part: ε'' = d/100 ε'

Find 1) the value of C and 2) the value of R. (20 points)

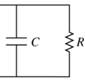
(Answer)

S = a cm² = 3 cm² = 3×10⁻⁴ m² , d = b/10 cm = 0.1 cm = 0.001 m

ε' = cε₀ = 9ε₀, ε'' = d/100 ε' = 0.04(9ε₀) = 0.36ε₀

1) (10 points)

C = ε' S / d = 9×(8.854×10⁻¹²)×( 3×10⁻⁴)/0.001 = 23.9 pF

2) (10 points)

R = d/[(ωε'')S] = 0.001/[2π(10×10⁶)×(0.36×8.854×10⁻¹²)× (3×10⁻⁴)] = 16.6 kΩ

3. Find 1) the conductor loss power density p_c (W/m³), 2) the dielectric loss power density p_d (W/m³), and 3) the dielectric stored power density p_e (W/m³) in a medium with

ε' = dε₀, ε'' = (c/100)ε', σ = (b/100) (S/m) , | E | = 10a V/m, f = 100a MHz (30 points)

(Answer)

ω = 2πf = 2π(100a×10⁶) = 600π×10⁶ Hz

| E | = 10a = 30 V/m

σ = b/100 = 0.01 (S/m)

ε' = dε₀ = 4ε₀

ε'' = (c/100)ε' = 0.009(4ε₀) = 0.036ε₀

1) (10 points)

p_c = (1/2)σ| E |² = 0.5×0.01×30² = 4.50 (W/m³)

2) (10 points)

p_d = (1/2)ωε''| E |² = 0.5×(600π×10⁶)×(0.036×8.854×10⁻¹²)×30² = 0.270 (W/m³)

3) (10 points)

p_e = (1/2)ωε'| E |² = 0.5×(600π×10⁶)×(4×8.854×10⁻¹²)×30² = 30.0 (W/m³)

4. Planewave

ε = dε₀, μ = aμ₀, f = 100b MHz

Find 1) the intrinsic impedance η, 2) the propagation constant k, and 3) the wavelength λ. (30 points)

(Answer)

ε = dε₀ = 4ε₀, μ = aμ₀ = 3μ₀, f = 100b = 100 MHz

1) (10 points)

η = (μ/ε)^1/2 = (3/4)^1/2 (μ₀/ε₀)^1/2 = (3/4)^1/2×377 = 326 Ω

2) (10 points)

k = 2πf (μ/ε)^1/2 = 2πf (3×4)^1/2 (μ₀ε₀)^1/2 = 2π×100×10⁶× (3/4)^1/2/(3×10⁸) = 0.181 rad/m

3) (10 points)

λ = 2π/k = 2π/0.181 = 34.7 m

5. Planewave reflection and transmission, normal incidence

ε₁ = bε₀, ε₂ = cε₀, μ₁ = dμ₀, μ₂ = aμ₀

Find 1) the reflection coefficient Γ and 2) the transmission coefficient τ. (20 points)

(Answer)

ε₁ = bε₀ = ε₀, ε₂ = cε₀ = 9ε₀, μ₁ = dμ₀ = 4μ₀, μ₂ = aμ₀ = 3μ₀

η₂ = (μ₂/ε₂)^1/2 = (3/9)^1/2 (μ₀/ε₀)^1/2 = (1/3)^1/2η₀

η₁ = (μ₁/ε₁)^1/2 = (4/1)^1/2 (μ₀/ε₀)^1/2 = 2η₀

1) (10 points)

Γ = (η₂ − η₁) / (η₂ + η₁) = [(1/3)^1/2 − 2] / [(1/3)^1/2 + 2] = −0.55

2) (10 points)

τ = 2η₂ / (η₂ + η₁) = 2(1/3)^1/2 / [(1/3)^1/2 + 2] = 0.45

6. Write a Python code for Problem 6. Submit your source code and the result of your program execution. (10 points)

(Answer)