ÃÊ°íÁÖÆÄ°øÇÐ Áß°£°í»ç ¹®Á¦ (2021-4-23,
15:00-15:50), eCampus¿¡ 15:50 ÀÌÀü±îÁö ´äÁö ¹®¼ ¶Ç´Â »çÁøÁ¦Ãâ
Çйø ( ) ¼º¸í (
) À̵¿ÀüȹøÈ£(
)
PIN = abcd: ÈÞ´ëÀüÈ ³¡ 4 ÀÚ¸® (¿¹: 010-8028-3194, a = 3, b = 1, c = 9, d = 4), ´Ü °¢ ¼ýÀÚ°¡ 0ÀÎ °æ¿ì ¼øÂ÷ÀûÀ¸·Î 1, 2, 3, 4·Î ´ëü (¿¹: 010-1234-0097ÀÎ °æ¿ì a = 1, b = 2, c = 9, d = 7)
¹èÁ¡: ¼Ò¹®Á¦´ç 10Á¡
1. Transmission line R, L, G, C
parameter calculation:
We have a
transmission line operating at 100 MHz with R
= a /1000 ¥Ø/m, L = 100b nH/m, G = c/1000
S/m, C = 10d pF/m. Write down a Python
code to calculate the following. Run it on www.online-python.com. Submit the source code and the result of your program execution by
capturing the PC screen.
1) the
characteristic impedance Z0
(¥Ø),
2) the
attenuation constant ¥á (Np/m),
3) the phase
constant ¥â (rad/m)
Hint: complex
arithmetic
math.sqrt(z):
take a square root of a complex number z
z.real: take
the real part of a complex number z
z.imag: take
the imaginary part of a complex number z
2. Input reflection coefficient, input impedance,
and delivered power:
A load ZL at z = 0 is connected with a tranmision line of length l with Z0 and ¥â.
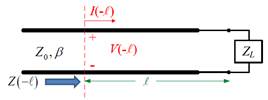
ZL = 10(d - jc) ¥Ø
Z0 = 10a ¥Ø
l = 0.2 wavelength (tranmssion line length)
Find at z = −l,
1) the load
reflection coefficient
2) the input
reflection coefficient ¥Ã(−l)
3) the input
impedance Z(−l) (¥Ø)
4) the power
delivered to the load when a power of 1 watt is incident on the transmissio
line at z = −l.
3. L, C parameters of a coaxial cable:
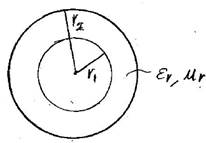
For a coaxial cable with
the radius of the center conductor r1 = a mm
the radius of
the outer conductor r2 = a+5b mm
the dielectric
constant of the material between the inner and outer conductors ¥år = c
the relative
permittivity of the material between the innder and outer conductos ¥ìr = d
find
1) the
inductance per unit lenght L,
2) the
capacitance per unit length C,
3) the
characteristic impedance Z0.
4. Impedance Smith chart, admittance Smith chart:
With Z0 = 10d ¥Ø,
1) draw R = 10a ¥Ø curve and X = −10b ¥Ø curve on the impedance Smith chart.
2) draw G = 1/(10c) S and B = 1/(10a) S curve on the admittance Smith
chart.
5. Conjugate matching:
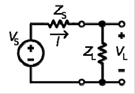
Zs = 10(a + jd) ¥Ø, VS = c exp(jb)
1) Find ZL for maximum power transfer
to ZL.
2) In this
case, find the power dissipated in ZL
6. A quarter-wave transformer:
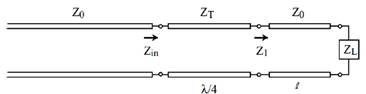
Z0 = 10d ¥Ø, Zin = 100a ¥Ø
¥ÃL: magnitude = c/10, phase = 20b deg.
1) Find the
minimum value of l in terms of the
wavelength on the transmission line.
2) Find the
input impedance Z1 in the
figure.
3) Find ZT.
7. LC
matching:
A load impedance ZL = 20c + j50d ¥Ø is to be transformed to Zin = Z0 = 30a ¥Ø at
100 MHz.
1) Use the Python code given
in the lecture webpage to find all possible LC
matching networks. Run it on www.online-python.com. Submit the source code and the result of your program execution by
capturing the PC screen.
2) Draw all of your
matching networks.
Hint: The Python code for
this problem is available on the lecture web page as 06-python.txt