제1장 벡터 수학

1. 1/1.2 벡터의 기초

벡터의 표기:　

벡터의 합과 차:

　 　

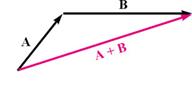
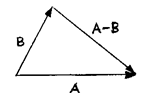
벡터 의 크기 표기: , ,

벡터와 스케일러의 곱:

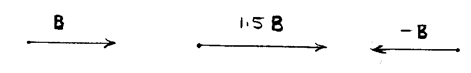
벡터 의 단위벡터:　

　　 방향은 벡터 의 방향과 동일. 크기는 1. 표기는 　또는

　　

1.3 직각 좌표계

직각좌표계(rectangular coordinate system = Cartesian coordinate system):

　　

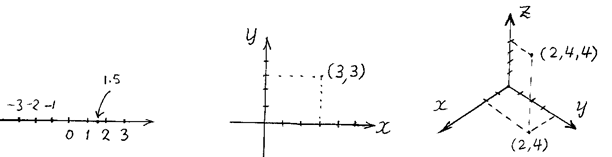
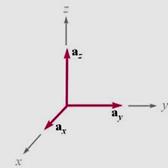
기본벡터(base vector): 등으로 표기　

오른손 법칙 적용 →> 축에서 축 방향으로 회전시 오른 나사가 진행하는 방향이 축

　 　

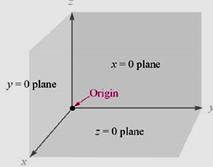
좌표면(coordinate surface): 서로 직교하는 3개의 평면

　　 평면:　 　평면이라고도 함.

　　 평면:　 　평면이라고도 함.

　　 평면:　 　평면이라고도 함.

직각좌표계의 점: 임의의 점의 좌표가 일 때 이 점은　 인 평면, 인 평면, 인 평면　 의 교점이다.　 원점에서 축 방향으로 만큼, 축 방향으로 만큼, 축 방향으로 만큼　 이동한 점이다.

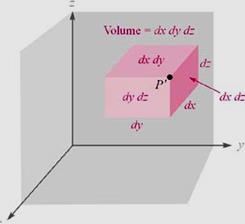
직각좌표계에서의 변화량(differential):

　　 : 좌표점

　　 : 극소면적(differential area)

　　 : 극소체적(differential volume)

　　 : 극소길이(differential length)

　　

　　　　　　　 　　　　　　　　　　

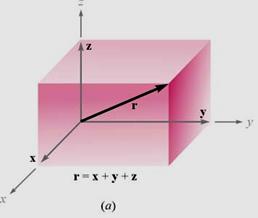
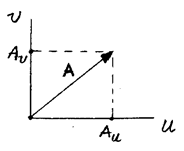
직각좌표계를 이용한 벡터 표시:

위치벡터:　 표원점으로부터 공간상의 점 으로 향하는 벡터. 표기는 다음과 같이 한다.

　　

　　 : 벡터의 성분표시(component form of a vector)

임의의 벡터:

　　

　　 : 벡터 A의 x 방향 성분

　　 : 벡터 의 방향 성분 크기

　　

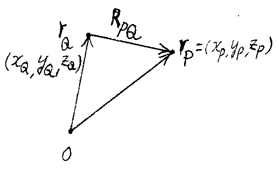
거리벡터(range vector):

점 에서 점 로 향하는 벡터(= 점 와 점 　사이의 거리벡터)

　　

　　

1. 4 성분을 이용한 벡터 계산

　　

　　

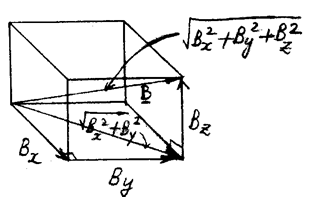
　　 : 벡터의 크기

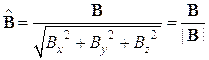　　 : 단위벡터

　　

　　

　　

1. 5 벡터장

　　 위치에 따라 값이 변하는 벡터함수를 벡터장(vector field)라 한다. 위치에 따른 풍속,　 전기장 세기, 자기장 세기 등이 벡터장의 예이다.

1. 6 내적

내적의 정의:

　　

내적 = dot product = inner product = scalar product

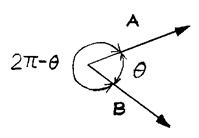
내적의 계산:

　　

　　

　　 　　　　

　　 　　　　　　　　　　　　　　　　　

　　 　벡터 와 벡터 는 직각(orthogonal)

　　

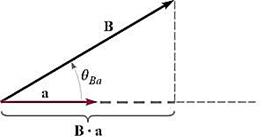
내적을 이용한 벡터의 성분 계산:

벡터 의 벡터 　방향 성분 = 투영(projection)

　　 　

서로 직교하는 임의의 두 방향 으로 벡터 를 분해하면

　　

　　

여기서 세 벡터 는 동일 평면에 있어야 한다.

　　 :　 벡터 의 방향 성분 크기

　　 :　 벡터 의 방향과 직각 방향 성분 크기

　　

1. 7 외적

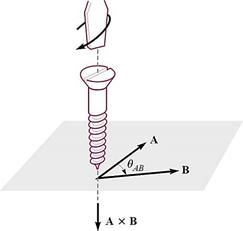
외적의 정의:

외적 = cross product = vector product

　　

　　 : 벡터 를 벡터 　방향으로 회전시킬 때 오른 나사(screw)가 진행하는 방향

　　 : 벡터 를 벡터 　방향으로 회전시킬 때 회전각

　　

외적의 계산:

　　

　　

　　 　

　　

　　

　　

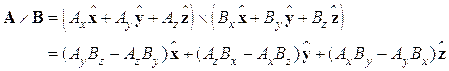
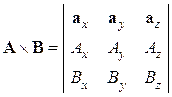
　　 : 두 벡터는 서로 평행

외적을 이용한 두 벡터에 수직인 벡터 계산:

　　

외적의 응용:

- 삼각형의 면적:

　　 　

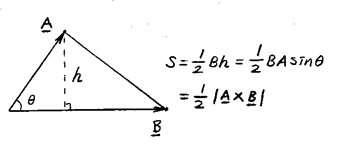
- 평행육면체의 체적:

　　 　

　　

　　

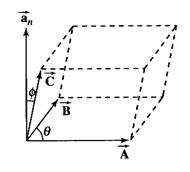
- Scalar triple product:

　　

　　 　　

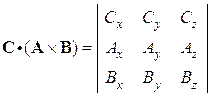
1. 8 원통좌표계

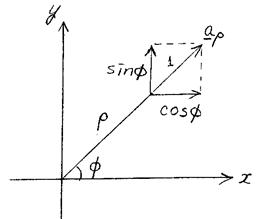
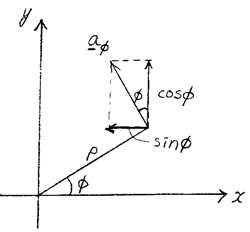
- 극좌표(polar coordinate):

　　 : ,

(예제) 직각 좌표계로 나타낸 점 (2,3)를 극좌표계로 나타내어라.

　　

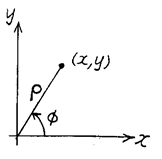
- 극좌표와 직각좌표의 관계:

　　

　　 　

- 극좌표와 복소수:

　　

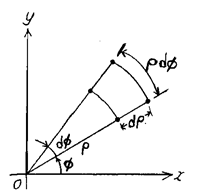
- 극좌표에서의 극소길이와 극소면적:

　　

　　

　　

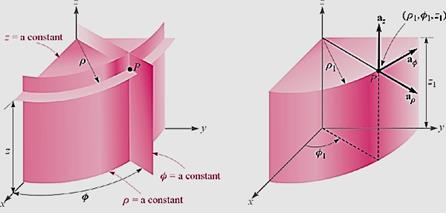
원통좌표계(cylindrical coordinate system):

- 좌표면:

　　 　면: 중심이 축과 일치하며 반경이 인 원통면

　　 　면: 평면을 축 방향으로 만큼 회전한 면

　　 　면: 평면을 축 방향으로 만큼 이동한 면

- 좌표축: 　= 원통좌표계의 기본벡터 (좌표축)

- 좌표점: , : 원통좌표계로 나타 낸 점의 좌표

　　

- 원통좌표계에서의 극소변화량:

　　

　　

　　

　　

　　

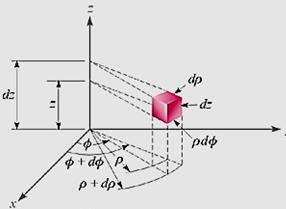
　　 : 극소 선분길이

　　 극소면적:

　　

　　

　　 　　

　　 : 극소체적

- 원통좌표와 직각좌표의 상호변환:

　　 　　

　　

　　

　　

　　

　　　　　 　　　　　　　　　　　

1.9 구좌표계(Spherical Coordinate System)

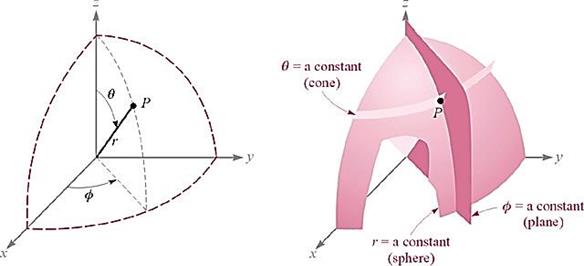
구좌표계의 정의:

- 좌표면:

　　 　면: 중심이 원점이며 반경이 인 구면

　　 　면: 중심이 축이며　 중심축으로부터 표면까지의 각도가 인 원뿔면

　　 　면: 평면을 축 방향으로 만큼 회전한 면

　　

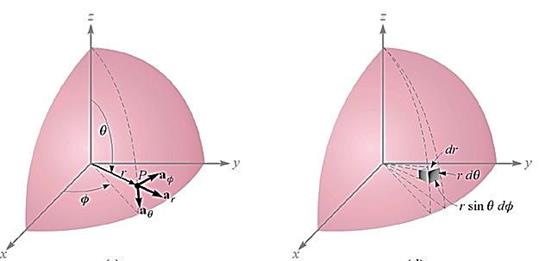
- 좌표축: 　　 =　 구좌표계의 기본벡터(좌표축)

- 좌표점: , : 구좌표계로 나타 낸 점의 좌표　　　

구좌표계에서의 극소변화량:

　　

　　

　　

　　

　　

　　

　　

　　

　　

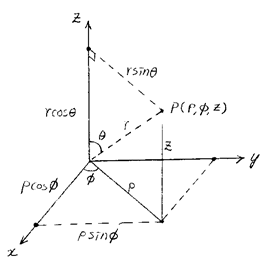
구좌표계와 직각좌표계의 상호변환:

　　 　　　　　

　　

　　

　　

　　

　

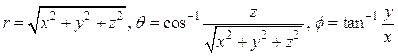
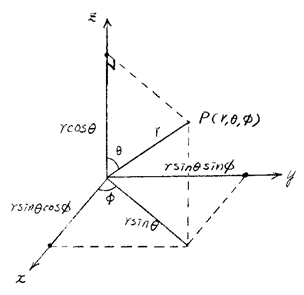
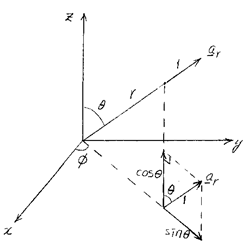
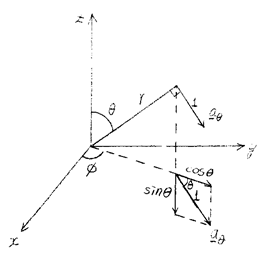
원통좌표계와 구좌표계와의 관계:

　　

　　

　　

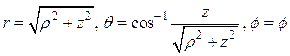
벡터의 좌표계 변환:

　　 (1)

를 에서

　　 (2)

로 변환하자.

우선 를 대입하여 를 구한다.

점 에서 구좌표계의 단위벡터 를 직각좌표계의 단위벡터 로 나타낸다.

　　

　　

　　

식 (1)에 위에서 구한 와 를 대입하여 를 기준으로 동류항을 정리하면 식 (2)를 얻는다.

.