실습-08 배열 안테나(Array Antenna)

 

단일 소자의 방사 패턴은 와 같이 너무 넓기 때문에 표적 감지 또는 원거리 통신 등 첨예한 빔 폭이 필요한 경우에는 적합하지 않다. 또한 다양한 모양의 방사 패턴을 구현하려면 방사 소자를 적절히 배치하여 배열(array) 안테나를 구현해야 한다.

 

안테나 배열은 방사 소자, 방사 소자 배치 방식, 방사 소자 급전 회로망 등으로 구성 된다. 배열에 사용되는 방사 소자는 급전이 용이할 뿐만 아니라 방사 패턴, 편파특성, 대역폭, 형상 등의 측면에서 가장 적합한 형태로 선정된다. 방사 소자로는 다이폴, 슬롯, 도파관 종단개구면, 혼 안테나, 스파이럴 안테나, 마이크로스트립 패치 안테나, 모노폴, 루프 등 다양한 종류가 있다.

 

방사 소자가 선정되면 다음 단계로 방사 소자의 배치 방식이 결정되어야 한다. 한쪽 방향으로만 첨예한 방사 패턴을 구현하려면 방사 소자가 일직선 상에 배열되는 선형배열(linear array) 구조를 사용한다. 원형 대칭성을 가지는 방사 패턴을 구현하려면 방사 소자를 적절한 크기의 원주 위에 배열한다. 이를 ring array라 보통 방향탐지 시스템에서 많이 사용되는 배열 방법이다. 양쪽 방향으로 모두 첨예한 방사 패턴을 구현하려면 방사 소자를 평면상에 2차원으로 배치하여야 한다. 배열 경계면은 사각형, 원형, 타원형, 삼각형, 사다리꼴 등의 형태를 가 진다. 평면상에 구현된 배열을 2차원 배열이라 한다.

 

I. 실습

1. 단일소자 설계: 16.15GHz 패치 안테나

1) 방사소자 형상 제시

ㅇ 좌표 축을 위의 그림과 같이 하라.

 

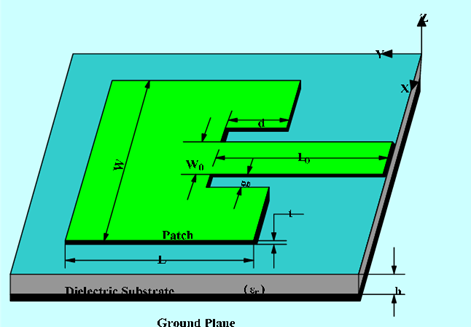
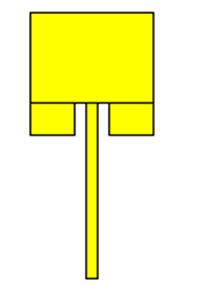
inset fed microstrip patch에 대한 이미지 검색결과   inset패치

                          (a)                                             (b)

그림: (a) Inset-fed 패치 안테나 설계변수[Mishra(2015, IEEE India Conf)]. (b) 16.25GHz 패치

 

기판 Taconic TLX-9: 두께 0.508mm, 유전상수 2.50, 손실탄젠트 0.001, 도체 두께 0.018mm (0.5 oz. copper), 기판크기 20x20mm

패치: 길이 L = 5.58mm, 폭 W = 5.49mm, 인셋용 제거 폭 W0 + 2g = 1.49mm, 인셋깊이 d = 1.8mm; 급전선 폭 W0 = 0.49mm(90Ω)

 

(참고)  16.25GHz에서 정확히 공진하지 않으면 frequency scaling 원리로 패치 길이 L을 미세조정하라.

 

ㅇ 인터넷 온라인 마이크로스트립 계산기 mcalc 사용: 주파수 분산, 손실포함

       http://mcalc.sourceforge.net/

 

ㅇ 마이크로스트립 wave port 크기: Microwave Studio를 이용하여 마이크로스트립 선로 해석 시 wave port의 폭은 스트립 폭의 6배 이상, 높이는 기판 두께의 4배 이상으로 설정. Wave port 내에 실제 마이크로스트립 전송선의 에너지가 95% 이상 포함되어야 한다. Wave port의 크기에 따라 마이크로스트립 선로의 특성 임피던스가 약간 씩 달라진다.

 

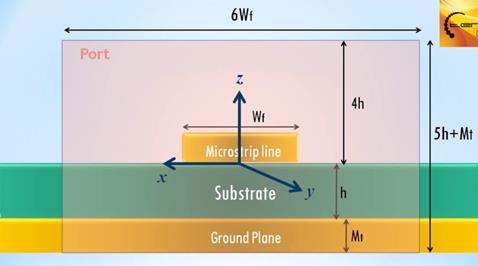
https://i.ytimg.com/vi/k54XWrcI5Bc/maxresdefault.jpg

 

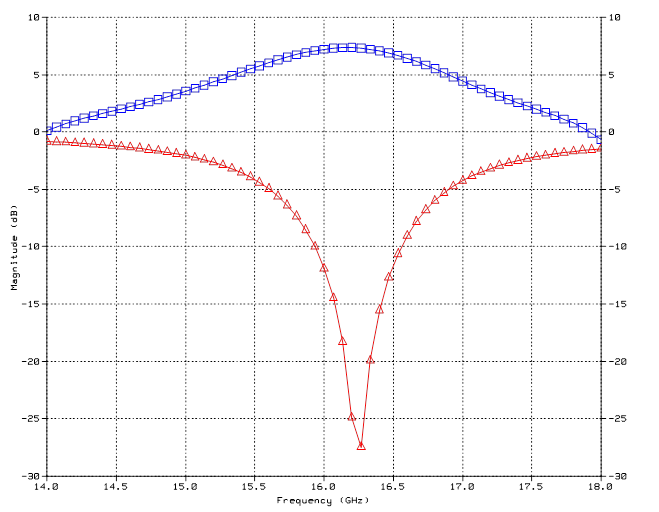
2) 반사계수 제시

-50dB to 0dB, 15-18GHz

- Ensemble 5.0을 이용한 계산결과

 

2) 전계면(yz-평면, phi = 90º) 정규화한 이득패턴

- Gtheta, -40dB to 0dB, Cartesian pattern, -90º to +90º

(참고) Ensemble 5.0을 이용한 계산결과

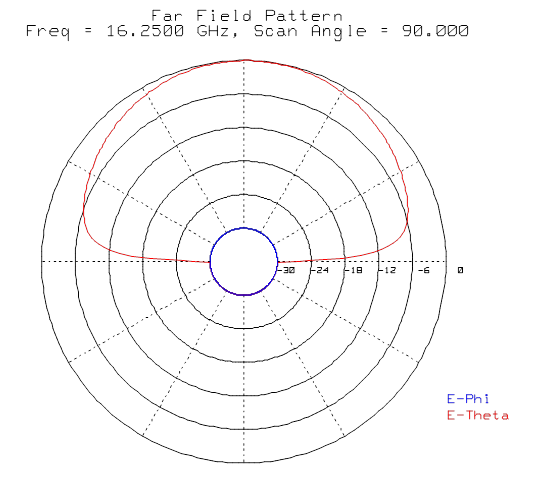
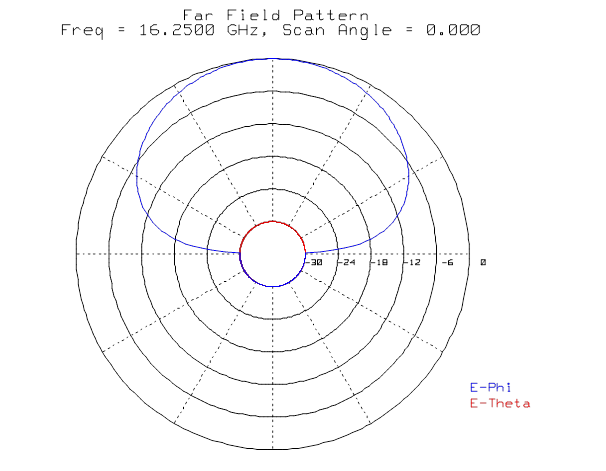
3) 자계면(zx-평면, phi = 90º) 정규화한 이득패턴

- Gphi, -40dB to 0dB, Cartesian pattern, -90º to +90º

(참고) Ensemble 5.0을 이용한 계산결과

 

5) 3차원 이득패턴

- 최대 이득 제시

 

2. 선형배열 설계

위에서 설계한 단일 소자를 자계면 방향(x 축 방향)으로 0.4875파장(9mm @ 16.25GHz) 간격(중심간 간격)으로 18개를 생성하라. Microwave Studio의 array 기능 이용.

 

그림: 18개 소자 패치 선형배열 안테나

 

배열 설계시 각도 θ의 정의: 배열 축 상의 오른쪽 방향(θ = 0º)을 기준으로 한 각도

      

     θ = 90º → 배열 축에 수직인 방향, θ = 180º → 배열 축 상의 왼쪽 방향

 

1) 주 빔이 θ = 124.75º (배열 축에 수직인 broadside 방향(θ = 90º)에서 1번 소자 방향으로 34.75º 스캔)가 되려면 소자간 위상차 α가 다음 조건을 만족해야 한다.

 

 

따라서 각 소자를 다음과 같이 급전하라.

1번: 크기 1, 위상 100º

2번: 크기 1, 위상 200º

3번: 크기 1, 위상 300º

4번: 크기 1, 위상 400º → 40º

5번: 크기 1, 위상 140º

6번: 크기 1, 위상 240º

7번: 크기 1, 위상 340º

8번: 크기 1, 위상 440º → 80º

9번: 크기 1, 위상 180º

10번: 크기 1, 위상 280º

11번: 크기 1, 위상 380º → 20º

12번: 크기 1, 위상 120º

13번: 크기 1, 위상 220º

14번: 크기 1, 위상 320º

15번: 크기 1, 위상 420º → 60º

16번: 크기 1, 위상 160º

17번: 크기 1, 위상 260º

18번: 크기 1, 위상 360º

 

(a) 배열 형상(모습, picture) 도시

 

(b) 자계면(zx-평면, phi = 0º) 방사패턴

- 패턴 도시: Cartesian, Gphi, -40dB to 0dB, -90º to 90º

- 주빔위치, 빔폭(3dB), sidelobe level, 격자엽 발생 각도 기록

 

(참고) Ensemble 5.0을 이용한 해석 결과: 이득 17.1dBi

 

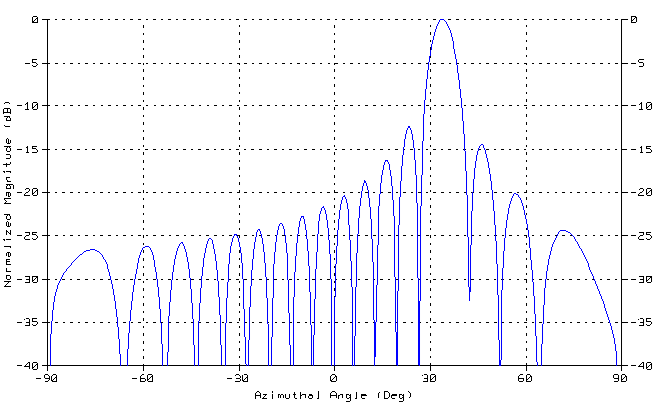
(c) 3차원 방사패턴

- 패턴 도시: Gabs, 각도 분해능을 2º로 설정

- 최대 이득 기록

 

2) 소자 전류는 그대로 두고 소자 간격을 17mm(0.921파장 @ 16.25GHz)으로 한 후 위 1)의 과정 반복

- 격자엽이 발생하는 각도 기록

 

3) 위 2항에서 소자 전류의 크기는 모두 1로 두고 위상을 모두 0º로 한 후 위 1)의 과정 반복

- 격자엽이 발생하는가?

 

4) 소자 전류 크기가 균일하면 부엽크기가 -13.3dB이다. 부엽을 줄이려면 소자전류를 중심에서 크게하고 양쪽에서 작게 해야 한다. 소자 위상을 0º로 동일하게 하고 소자 전류 크기를 다음과 같이 설정한 후 위 1항을 반복

     1번: 0.2, 2번: 0.3, ...., 9번: 1.0, 10번: 1.0, 11번: 0.9, ..., 18번: 0.2

     단, Cartesian 방사패턴 계산시 수직 축 -60dB to 0dB로 하라.

 

II. 이론

1. 배열인자

ㅇParallel-ray approximation

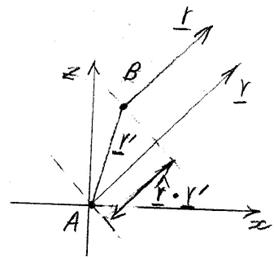
그림: 방사소자의 원거리 전기장 계산

 

- 점 B에 있는 소자 B의 원거리 전기장

 

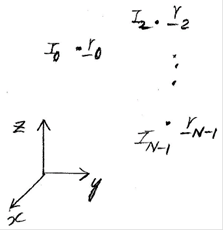
그림: 소자가 임의로 배치된 배열

 

 : 소자 전류

 : 소자가 위치하는 점의 좌표벡터

- 위 그림과 같이 N 개의 동일한 방사소자가 동일한 자세로 배치되어 방사될 경우 배열인자

 

 

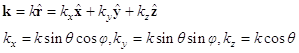
- 특정 방향으로 최대 방사가 일어나기 위한 조건

 

 : k 번째 소자 전류(전압)의 크기(amplitude)

 : k 번째 소자 전류(전압)의 위상(phase)

 

 

2. 패턴 곱의 원리(Principle of Pattern Multiplication)

- 배열의 방사패턴 = 방사소자 방사패턴 × 배열인자

: 배열 안테나의 방사패턴

: 방사소자의 방사패턴

: 배열인자

 

 : 단일 방사소자의 지향도

 : 배열인자에 의한 지향도

 

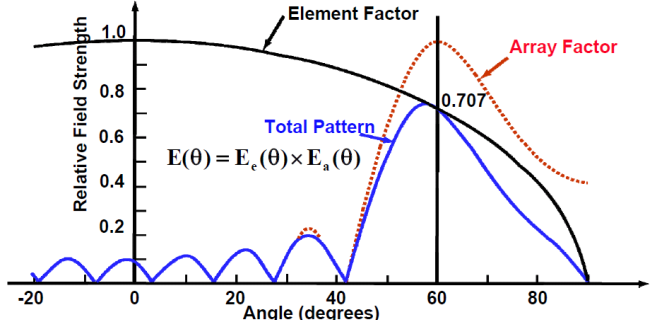
그림: 패턴 곱의 원리[O'Donnell]

 

3. 선형 배열(linear array)

선형배열은 안테나 배열의 기초를 학습하는 데에 도움이 된다. 선형배열 이론을 잘 파악하면 2차원 배열, 3차원 배열, 곡면배열 설계 시 유사한 원리를 적용하여 설계할 수 있다.

 

1) 선형 배열의 기초

ㅇ 축상에 배열된 선형 배열 안테나

    

2-1

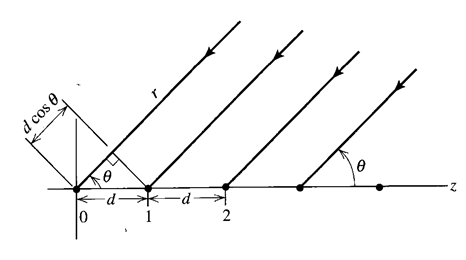
그림: 선형 배열 안테나

 

ㅇ z 축상에 일정한 간격 d 을 두고 N 개의 방사 소자가 배열될 경우 배열인자

    

    

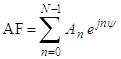
     , An = 전류 크기, nα = 전류 위상

 

ㅇ 주 빔이 에 위치할 경우(beam scanning)

    

      : 각 소자간 위상차

 

(중요) 위상이 감소하는 방향으로 주 빔이 tilt된다.

 

2) 측방사 배열과 축방사 배열

- 측방사 배열(broadside array): 배열의 주 빔이 배열 축에 수직. 소자간 위상차 α = 0º

- 축방사 배열(endfire array): 배열의 주 빔이 배열 축 방향. 소자간 위상차 α = –βd (+z 축 방향으로 방사), α = βd (–z 축 방향으로 방사)

- 주사 배열(scanned array): 주 빔에 배열 축으로부터 θ0 만큼 scan된(tilt된) 배열. 소자간 위상차 α = –βdcosθ0

 

          

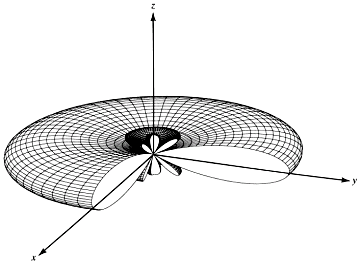
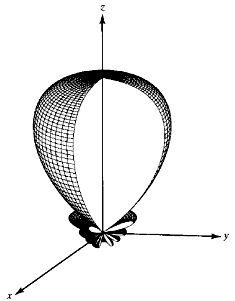
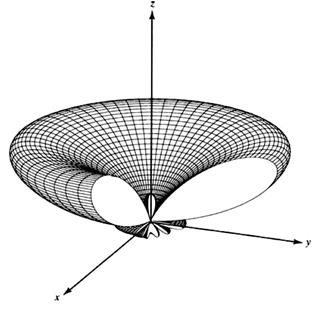
                  (a)                                     (b)                                           (c)

그림: z-축 상에 배열된 선형배열 안테나의 방사패턴. (a) 측면방사, (b) 종단방사, (c) 주사배열(θ0 = 60º)[Balanis]

 

3) 선형배열의 배열인자

ㅇ 균일하게 여기된 선형배열 안테나

      

    

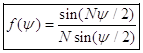      : normalized array factor

 

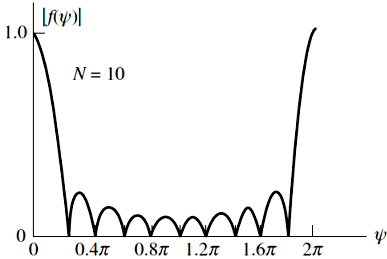
그림: 등간격 균일급전 선형배열 안테나의 정규화한 배열인자[Stutzman]

 

ㅇ의 특징

     주기: 2π

     우함수

     π를 기준으로 좌우 대칭

     주빔 영점 간 간격:  

     부빔(minor lobe)  영점 간 간격:

 

ㅇ 배열인자의 도식적 해법

- 주사배열

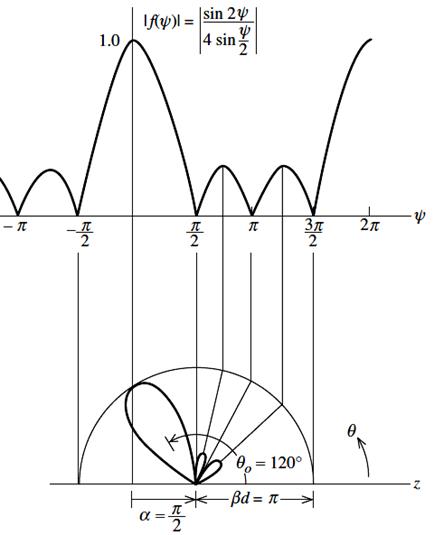
그림: 배열인자 도식적 해법. N = 4, α = π/2, d = λ/2 [Stutzman]

 

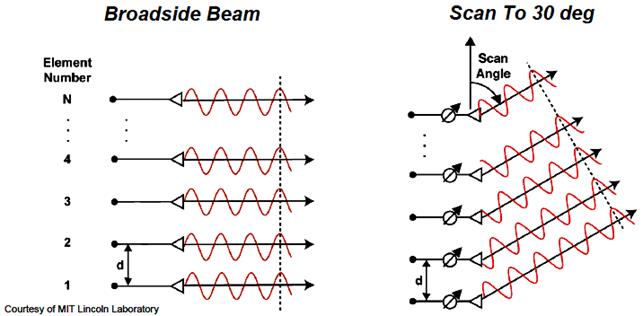
그림: 주사배열 개념[O'Donnell]

 

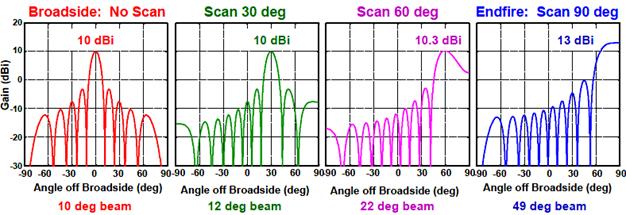
그림: 안테나 주 빔 주사. N = 20, d = λ/4

 

ㅇ 가시영역(visible region), 격자엽(grating lobe), 소자 간격 조건

- 가시 영역인 에서 격자엽(grating lobe)의 일부라도 나타나지 않게 하려면

    

    

 

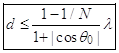
- 격자엽: 배열소자 간 간격이 과다하여 추가로 발생하는 major lobe. 1개 또는 다수 발생 가능

- 계산 예:

- 격자엽 발생 사례:

 

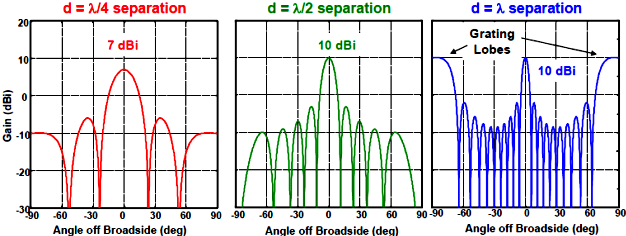
                                        (a)

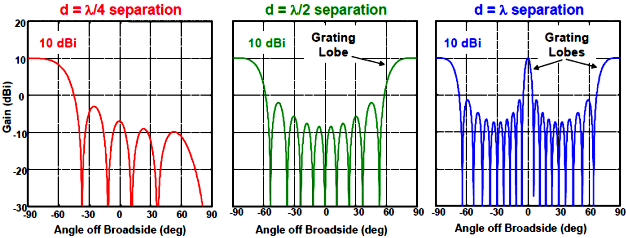
                                        (b)

그림: 방사소자 간격에 따른 배열인자. N = 10. (a) Broadside array (α = 0), (b) Endfire array (α = kd)

 

II. 연습문제(숙제)

1. 3GHz에서 동작하는 10개 소자 선형배열을 설계하라. 방사소자 방사패턴: 등방성

a) 최대 방사가 배열 축에 수직인 방향(θ0 = 90º)이며 grating lobe가 일부분이라도 가시영역에 나타나지 않도록 소자 간격을 결정하라.

b) 최대 방사가 배열 축에서 45º인 방향 방향(θ0 = 135º)이며 grating lobe가 일부분이라도 가시영역에 나타나지 않도록 소자 간격을 결정하라.

c) 위 b의 경우 방사패턴 polar 형식으로 도시하라.

 

III. 배열 안테나 사례