Physics of Free Fall

[Introduction]

Application: skydiving, parachute jump, air dispensing of flyers (pamplets).

Example: On 14 October 2012, Austrian skydiver Felix Baumgartner landed in eastern New Mexico after jumping from a world record of 128,097 feet (39.045 km), which he climbed to with a helium balloon. Maximum speed = 372.8 m/s and time taken = 4'19" = 259 s (including parachute fall time). He wore a pressured space suit.; Without air drag, the fall time would be 89.2 seconds with a final speed of 874.8 m/s.

[Theory]

Free-fall without air drag:

Force acting on a free-falling object

: downward force on a free-falling object

W = mg : weight (N), g = 9.8 m²/s (gravity)

Drag equation:

: (air) drag (force) (N). Lord Rayleigh's drag equation. For an object moving through a fluid at relatively large velocity

(i.e., high Reynolds number, R_e > 1000)

C_d: drag coefficient, dimensionless. 0.25–0.45 for a car. Depends on the Reynolds number. It varies with air density and the object

velocity.

ρ: air density (kg/m³)

v: the object's free-fall velocity (m/s)

A: the object's frontal area (m²). Reference area = area of the orthographic projection of the object.

For low Reynolds numbers, the drag is proportional to the object velocity.

Reynolds number: a dimensionless number that gives a measure of the ratio of inertial force to viscous forces and consequently

quantifies the relative importance of these two types of forces for given flow conditions.

Equilibrium velocity (= terminal velocity):

Equation of motion: assuming constant air density.

Example: 1.225 kg/m³ at sea level and at 15°C. We take 0.6 kg/m³_. Cd = 0.5, W= 100 kg, A= 0.1 m².

P. A. Tipler, College Physics, New York: Worth, 1987, p.105: "For a skydiver with parachute closed, the terminal velocity is about 200 km/m." 56 m/s.

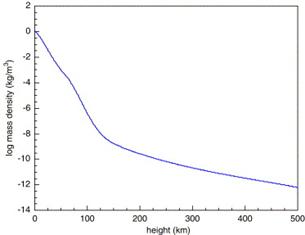
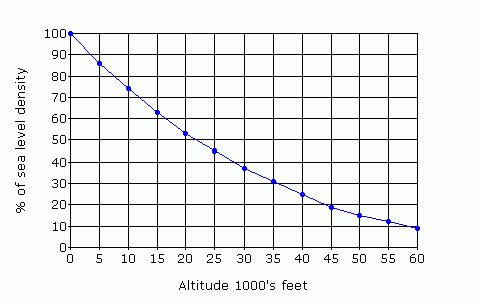
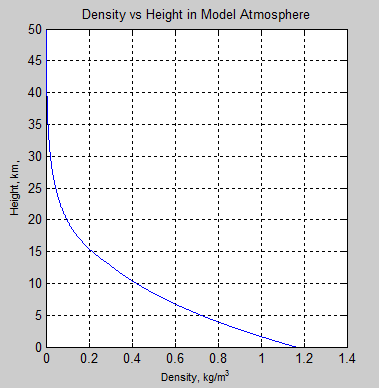
Troposphere: density and pressure model. 1976 International Standard Atmosphere (ISA) model

H(km) = 44.3308–42.2665 ´ D^0.234969; D air density in kg/m³.

H(km) = 44.3308–4.94654 ´ P^0.190263; P air pressure in Pa.

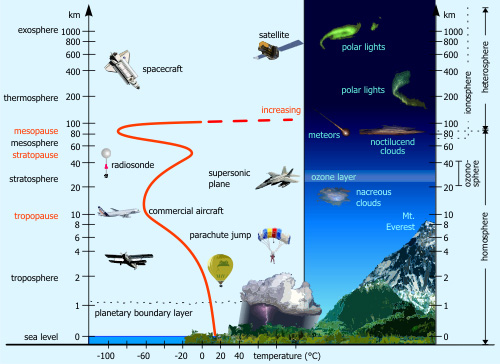
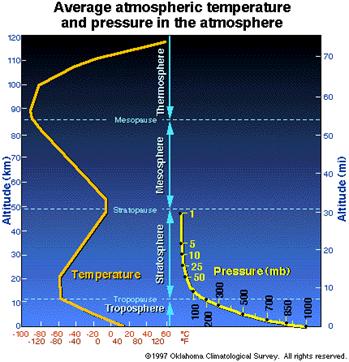
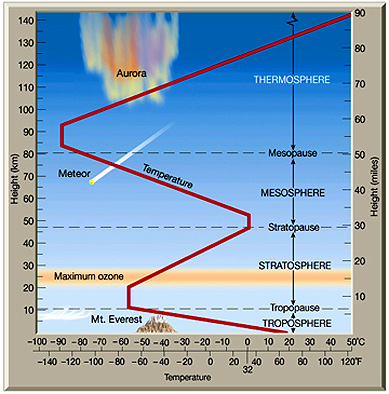
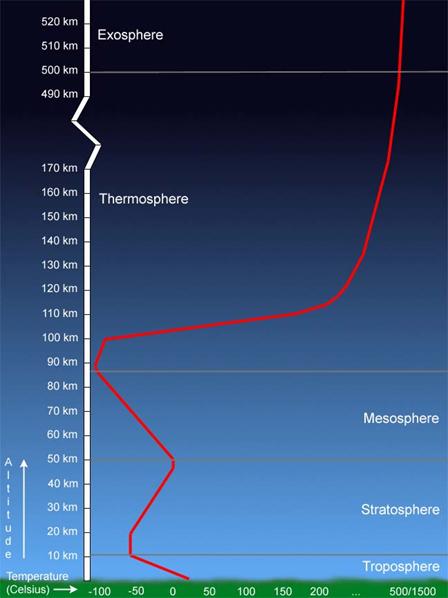
Air pressure:

1976 ISA Model: 0 ≤ h ≤ 11,000

1. Temperature

Troposphere: 10°C to –60°C linearly decrease.

Tropopause: –60°C, 11,000 ≤ h (km) ≤ 20,000

Stratosphere: –60°C to 0°C linearly increase. 20,000 ≤ h ≤ 50,000

StratopauseMesopause: -0°C, 50,000 ≤ h ≤ 55

Mesosphere: 0°C to –90°C, 55 ≤ h ≤ 85

Mesopause: –90°C, 85 ≤ h ≤ 90

Thermosphere: http://www.windows2universe.org/earth/Atmosphere/thermosphere_temperature.html&edu=elem

–90°C to –80°C , 90 ≤ h ≤ 100

–80°C to 175°C, 100 ≤ h ≤ 110

Solar max: day = 1055°C, night = 825°C

Solar min: day = 545°C, night = 315°C

11-year sun spot cycle

24-hour temperature graph

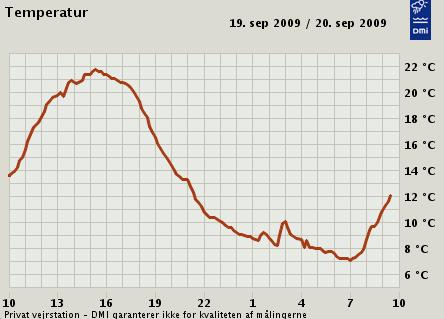
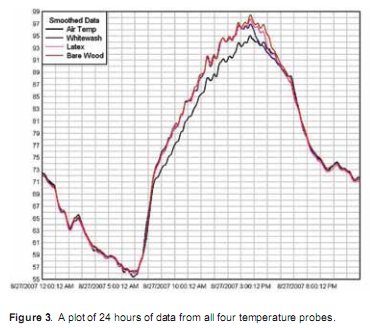
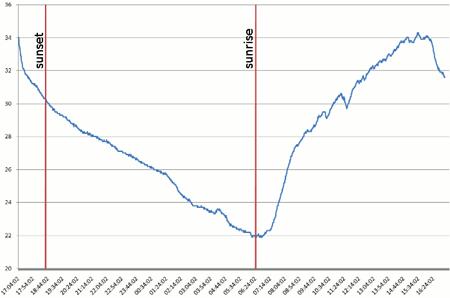
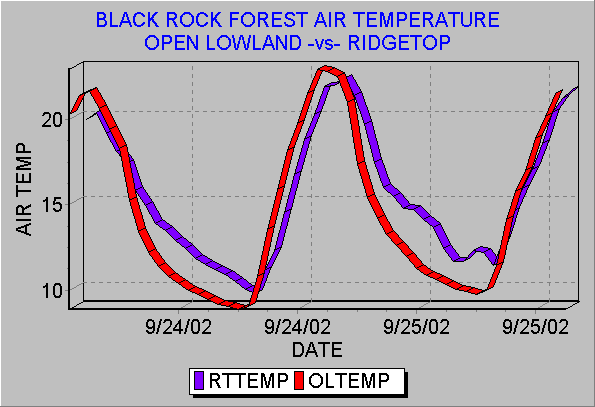
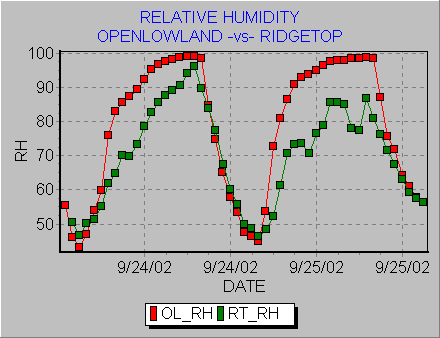
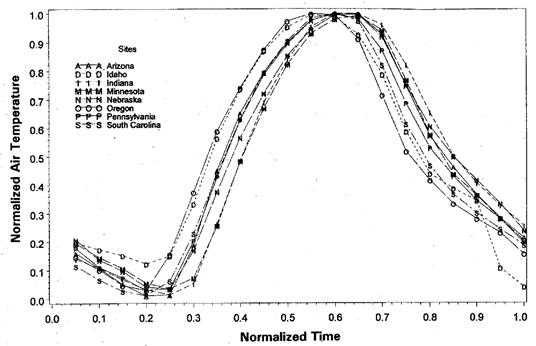
Beta distribution function:

Diurnal temperature model:

Cheongju City (1981-2010) average: min temp./max. temp./time of max. temp

Jan: -6.9/2.9/15:00; F -9/2 M -8/4

Feb: -4.6/6.0/15:00; F -6/6 M -4/8

Mar: 0.2/11.9; F -2/11 M 2/15

Apr: 6.1/19.5; F 5/15

May: 12.3/24.4; F 11/23

Jun: 17.6/27.9; F 16/27

Jul: 21.8/29.8; F 21/28

Aug: 22.0/30.5; F 21/29

Sep: 16.2/26.3

2.5, 3.5, 3.0

Oct: 8.5/20.7

Nov: 1.7/12.7

Dec: -4.3/5.6; F L-9/2

Program: year, moth, day, time, solar position

,000

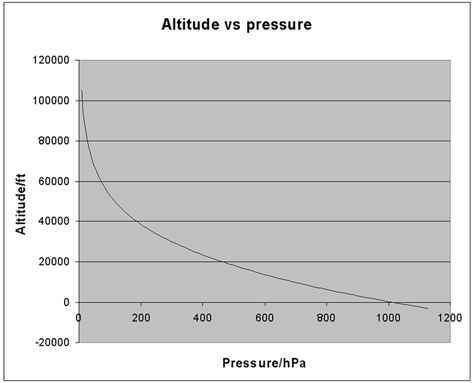
2. Pressure

P: pressure at the altitude of h (N/m² = hPa)

P₁₁ = 226.32 hPa (pressure at the toropause)

T₁₁ = 216.65 K (kelvin temperature at the toropause)

h: height above the sea level (m)

h₁₁ = 11,000 (m)

3. Air density

: air density (kg/m³)

R = 287.04 m²/Ks²

Air density

Exact solution: use numerical methods with exact parameter values.

[Numerical Solution]

To be added.

[Computer Code]

To be added.

[References]

Kiusalass, J., Numerical Methods in Engineering with Python, 2nd Ed., Cambridge U. Press, 2010.

Meade, D. B. and A. A. Struthers, "Differential equations in the new millennium: the parachute problem," In. J. Eng. Ed., Vol. 15, No. 6,

pp. 417–424, 1999; a UK journal.